Dosier: Didáctica de las Matemáticas.
Un análisis político e ideológico sobre saberes y prácticas

Mirar las matemáticas desde una perspectiva antropológica

Introducción

De¹ mis días de estudiante de matemáticas, tanto en la escuela como después en la facultad, no pueden dejar de venirme a la memoria dos sensaciones, tan claras como imposibles de separar: sensación de fascinación, sensación de temor. La rotundidad con que los conceptos y las demostraciones caían sobre la pizarra, de la mano que empuñaba la tiza con toda firmeza, los hacía súbitamente presentes como si de auténticas apariciones se tratara. El cielo se había abierto y de él caían, primero, números racionales y raíces cuadradas; más tarde, números imaginarios y grupos abelianos. Animadas por ellos, las demostraciones se precipitaban en cascada, con la misma inexorabilidad que la fuerza de gravedad, hasta que -¡oh, maravilla!- la pizarra temblaba con el tronar del “q.e.d.” (“quod erat demonstrandum”, o sea, “como se quería demostrar”) que el maestro clavaba en ella (cada uno de sus tres puntos, un clavo en mi mirada atónita). Y ¡voilà!, ahí, siempre en la esquina inferior derecha de una pizarra atiborrada de signos, aparecía el resultado.

Buena parte de mis pesquisas posteriores han estado orientadas, a menudo sin yo mismo saberlo, a ahuyentar aquel temor sin por ello espantar también el deleite que procura esa fascinación que tan bien conoce todo el que se ha dedicado a las matemáticas. La fórmula la encontraría mucho más tarde condensada, con esa envidiable precisión propia de las fórmulas verbales populares, en un antiguo cante gitano: “Voz del pueblo, voz del cielo”.

Efectivamente, esa multitud -que no conjunto- de operaciones, conceptos y prácticas a la que llamamos matemáticas no cae del cielo, sino que ha emergido y se ha ido modelando en ciertos momentos singulares y en ciertos lugares concretos. Y lo ha ido haciendo en las lenguas vernáculas que los matemáticos compartían con el común de sus vecinos y basándose en los mismos mitos y creencias que también compartían con ellos. Aquel cielo resultó ser el pueblo, los diferentes pueblos. El temor se trocó en confianza, en autoconfianza. Y la fascinación quedó intacta, aunque cambió el objeto que la provocaba. Lo fascinante ya no era aquel asombroso autodesplegarse de un lenguaje singular, reservado sólo a algunos expertos, sino la propia lengua, el castellano que hablábamos yo y mi gente, el griego que hablaban Euclides y su gente, el chino que hablaban Liu Hui y su gente, esa lengua corriente y moliente que, precisamente por su correr y moler, produce maravillas de continuo: mitos, dichos, leyendas, canciones… y matemáticas.

Aunque esta afirmación pueda parecer una obviedad para algunos, a otros les puede sonar a puro despropósito. De hecho, no ha empezado a calar entre los profesionales (docentes o investigadores) hasta los últimos veinte años. Incluso hoy, en las aulas de nuestras escuelas y universidades es habitual que las matemáticas sigan presentándose desnudadas de cualquier arraigo en el tiempo y en el espacio, desgajadas de las ocasiones, las circunstancias y las lenguas a las que deben el ser como son, y no ser de otra manera. Y ello pese a que, como he podido comprobar en muy distintos países y públicos, al presentarlas de este modo, el estudiante no sólo suele sentir un hondo alivio, sino también una comprensión mucho más profunda y, a menudo, ve estimuladas sus inclinaciones más creativas. Alivio, pues descubre que sus dudas, perplejidades y tanteos son los mismos que los que experimentaron los grandes “genios” matemáticos; que el bloqueo cognitivo o la obcecación en un razonamiento “erróneo”, que con tanta frecuencia le asaltan ante un desarrollo matemático, no son muy diferentes de los que han dejado sin saber qué pensar a las mejores cabezas del álgebra o la geometría, tan cargadas de prejuicios y presupuestos como él. Comprensión y estímulo creador, pues cae en la cuenta de que son su propia lengua y sentido común los que, en vez de incapacitarle para entender el lenguaje matemático (como tan a menudo se le inculca), le ponen en condiciones de entender su lógica subyacente (que no es matemática, sino lingüística y cultural), de percibir sus límites y, en consecuencia, de poder intuir otros enfoques si es capaz de imaginar otras metáforas.

Por todo ello, atender a las circunstancias históricas, antropológicas, lingüísticas y culturales en cuyo seno han ido cobrando las matemáticas su forma actual, lejos de limitarse a aportar un mero envoltorio que las presente más adornadas, puede ofrecer un caudal de estímulos y sugerencias, tanto para el estudiante como para el investigador. Conocer las dudas y tanteos de “los grandes matemáticos”, así como las razones por las que se decantaron por una solución y rechazaron otras, no puede sino darles –y darnos- confianza y ofrecerles –y ofrecernos- estrategias para poner en marcha cuando cada uno se encuentre en situaciones semejantes. El investigador, además, puede encontrar en ese distanciamiento al que obliga un acercamiento histórico o antropológico la perspectiva necesaria para reenfocar el problema desde otra perspectiva o reencuadrarlo en un nuevo marco donde adquiera otro sentido cuando, en el marco habitual en que se había encerrado, parecía carecer de solución.

El camino (en griego, méthodos; en chino, tao o dao) que me llevó, sin apenas quererlo, de las matemáticas como voz del cielo a las matemáticas como voz del pueblo se perfila en el que me transportó desde un estudio comparativo de las matemáticas chinas y griegas (Lizcano, 1993) hasta la investigación del lenguaje –y, en particular, de las metáforas que de continuo usamos sin saberlo- como creador de realidad, incluida esa realidad particular que son las matemáticas (Lizcano, 2006).

Lo simbólico como dispositivo de conocimiento

Los símbolos matemáticos no resultan ser esos meros signos que nos han acostumbrado a ver y que tienen su función en la comunicación social. Parece interesante considerar la idea de “auténticos símbolos” en el sentido que dan al término disciplinas como la hermenéutica o la antropología cognitiva. Así, para Dan Sperber (1978), lo simbólico no consiste tanto en un repertorio de objetos (símbolos) a interpretar o utilizar, sino en un dispositivo de conocimiento. Este dispositivo simbólico no actúa sobre unos símbolos predefinidos, a los que interpretaría o deconstruiría, sino sobre problemas o situaciones para los que no hay conceptos elaborados; se trata entonces un dispositivo de construcción de significado.

Por ejemplo, a la hora de intentar pensar un olor, para el que carecemos de un repertorio semántico y conceptual adecuado, se produce un triple movimiento, a la vez afectivo e intelectual: la focalización en una imagen, sensación o concepto que funciona como co-relato analógico del olor que se quiere pensar; una cascada de evocaciones convocadas por el poder atractor de aquel foco sobre el cual vienen a precipitar; un regreso al olor inicial, que resulta así iluminado y modelado por la imagen sobre la que el olor se había focalizado: la imagen se erige así en símbolo de aquel olor que la ha evocado. Supongamos que el olor que percibimos y que queremos conceptualizar sea el olor del incienso. La imagen sobre la que se focalizará, para quien pertenece a una cultura católica, seguramente será la imagen de una iglesia. Sobre esa imagen-símbolo precipitarán sensaciones y conceptos que evocan gravedad y respeto, silencio y recogimiento, tal vez también compenetración colectiva y la vivencia de una fuerza especial. Todas ellas contribuirán a dar forma al olor, a ponerle nombre: un olor grave (por la sensación de gravedad y respeto), un olor sordo (por el silencio evocado) o un olor embriagador (por la embriaguez colectiva de la liturgia) y penetrante (por la experiencia de sacralidad). Este proceso involucra y entrelaza registros cognitivos, emocionales, culturales, lingüísticos. Se correspondería más o menos con las operaciones de desplazamiento y condensación que considera Freud, así como con los dispositivos metafórico y metonímico que para Jakobson estructuran cualquier lenguaje. Desde esta perspectiva, es el proceso simbolizador -y no la matemática, según el proyecto leibniziano- el que está en el origen de todo lenguaje. Y, en particular, en el origen del lenguaje matemático y lógico. El proceso del matemático que se enfrenta a una situación para la que aún no tiene un concepto apropiado es semejante al de los olores.

A continuación, presentaré sintéticamente algunas indagaciones realizadas a partir de un modelo de análisis antropológico basado en el dinamismo de las metáforas que puede aplicarse al estudio y a la comprensión de construcciones matemáticas (Lizcano, 1999; 2009a; 2009b).

El origen de la raíz cuadrada

Imaginemos a un geómetra de la Grecia clásica que conoce el área de un cuadrado y se pregunta por la longitud de su lado. ¿Qué imagen le resulta evocada de manera inmediata? Aunque hoy nos pueda parecer increíble, la imagen que le viene a la cabeza es la de la raíz de una planta. Focaliza el cuadrado como un vegetal y su lado como la raíz de la que el cuadrado se alimenta: la raíz-lado, al desplegar toda su potencia (dynamis), engendra al cuadrado. El cuadrado es la potencia (cuadrada) del lado, aquello que el lado-raíz puede llegar a dar de sí. La siguiente imagen podría ayudar a organizar este análisis.

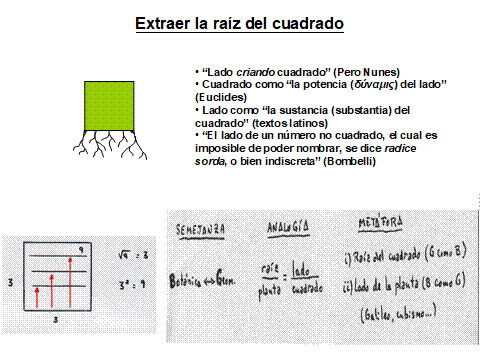
Por eso, para calcular el lado, hablamos todavía hoy de extraer la raíz del cuadrado o extraer la raíz cuadrada. Y así, la situación inicial que intentábamos pensar (el lado del cuadrado), al adquirir forma (forma de raíz) resulta ya pensable y el problema (calcular su longitud) se hace un problema resoluble.

En cada problema matemático aún sin resolver, en el origen de cada concepto cuando aún no lo era, fracasa la conceptualización anterior igual que fracasa nuestro repertorio enciclopédico ante los olores. Y cada una de estas situaciones puede pensarse en términos de un proceso de simbolización.

De hecho, cada una de las situaciones en que el antropólogo observa la actuación de dispositivos simbólicos en sociedades primitivas apenas difiere de las análogas en las tribus de matemáticos y epistemólogos. El que se hayan impuesto las matemáticas de la “tribu europea” no habla tanto de su superioridad lógica o formal, cuento de su mucho mayor apoyo político y difusión cultural. El tratamiento que sufre el problema de los olores es análogo, como hemos visto, al sufrido por el problema de la “raíz cuadrada”, y lo es también al que sufrirán los ensayos de conceptualización del cero (como veremos a continuación), de los números negativos, los irracionales o los infinitesimales, que han llenado de divertidos errores, de retórica y de poesía las páginas de los mejores matemáticos (en matemáticas -decía Wittgenstein- son tretas gramaticales las que nos convencen).

Conceptualizaciones acerca del cero

Intentaremos ahora aplicar esta metodología de análisis a aquel objeto matemático que ni siquiera el llamado programa fuerte de sociología del conocimiento científico (Bloor, 1998), pese a toda su potencia, era capaz de explicar: el cero. Y lo haremos en dos contextos sociales e históricos bien diferentes, para observar cómo los dispositivos simbólicos que se ponen en marcha son, en cada caso, también radicalmente distintos.

Algo que hoy llamaríamos un “cero”, cuando aún estaba sin conceptualizar es un blanco ideal para la actuación de dispositivos simbólicos, pues:

• se trata de una expresión sin referente aparente (¿cuál sería el referente de nada?), de una situación aún sin nombre,

• conduce a todo tipo de paradojas (como las de dividir por cero; o la de encontrarle sentido a la expresión “hay cierto número de personas” para significar que no había nadie: si “cero” fuera un número, esa expresión tendría sentido aún cuando no hubiera nadie, aunque tal vez a quien la profiriese le dirían que no sabe lo que dice),

• no existe caracterización en el repertorio matemático durante siglos,

• incluso cuando por fin resulte definido, seguirá siendo un concepto mal comprendido (seguramente hasta la elaboración de la moderna teoría de grupos).

Cada problema que históricamente ha venido rodeando a –lo que llamamos hoy- el cero, recorre los procesos simbólicos que distingue Sperber (1978):

• el problema se va focalizando, por desplazamientos metafóricos, en torno a conceptos vecinos (vacío, no-ser, caos… en Europa) o a otros símbolos ya cristalizados (Tao, Hun-tun… en China).

• estas focalizaciones dispararán un complejo de evocaciones inconscientes del repertorio de significados de cada sociedad: evocaciones conceptuales (inextenso), afectivas (horror, carencia), valorativas (la falta como defecto), gramaticales (partículas y sufijos negativos y privativos) o técnicas (suma, resta, técnicas numéricas, métodos de resolución de ecuaciones).

• estas evocaciones se proyectan (de distinto modo en cada contexto social e histórico) en los diferentes ensayos de conceptualizarlo formalmente, de operar con él, o de rechazar la mismísima posibilidad de que pueda existir algo semejante...

En la Grecia clásica, el texto que más aproximadamente evoca algo como nuestro cero pertenece al libro IV de la Physica de Aristóteles. Este texto se encuentra entre los muchos argumentos con los que Aristóteles intenta espantar racionalmente el pánico al vacío, y dice así:

Pero no hay ninguna razón en la que el vacío (kenón) sea excedido por los cuerpos, de igual modo que “nada” (mèdén = nada hay que) no está en razón alguna con un número. Pues 4 excede a 3 en 1, y a 2 en más (que 1), y a 1 en todavía más de lo que excede a 2; pero cuando llegamos a nada (mèdenós) no hay razón alguna en la que 4 lo exceda, pues el número que excede debe dividirse en el exceso y el número que es excedido, así que 4 debería ser la suma del exceso y nada (aquí oudén, no mèdén: no hay concepto para ese “nada”). Por esto, tampoco una línea excede a un punto (en ninguna razón), porque no está hecha de puntos. Similarmente, el vacío no puede estar en razón alguna con lo lleno.

En el texto se presenta un razonamiento por analogía, una demostración por reducción al absurdo y una apelación al prestigio de las matemáticas para consolidar un pre-juicio común a toda la tribu.

Se trata de un razonamiento analógico: el vacío, si existiera, sería a los cuerpos lo que nada es a los números (vacío/cuerpos = nada(no) / números). Aunque Aristóteles ha denunciado repetidamente la legitimidad de las demostraciones por analogía, aquí lo hace. Todo vale si le permite dar forma aparentemente lógica a la demostración (!) de un prejuicio: ese horror al vacío que también nosotros hemos heredado de aquellos griegos.

La demostración es “por reducción al absurdo”: si hubiera una relación (sumativa) entre el vacío y los cuerpos habría de ser como la que habría entre nada y los números. Pero, como es impensable que haya una relación entre nada y número, hemos de concluir que tampoco puede haberla entre el vacío y los cuerpos. Como tan lúcidamente han puesto de manifiesto Ortega y Gasset (1979) y Szabó (1964 a y b), todo razonamiento de este tipo va llevando al lector/oyente a una situación que es evidentemente imposible, es decir, que éste considera incompatible con los principios compartidos por toda la tribu: lo que “todo el mundo sabe”. Y, como nadie querrá verse excluido del grupo, no le cabe otra opción que admitir la imposibilidad del supuesto de partida que le había llevado a tan desagradable coyuntura. El razonamiento matemático sobre el que descansa la demostración (4 = 3+1, 4 = 2+2, 4 = 1+3, 4 = mèden+4) no es ni siquiera un razonamiento. Se inicia una serie que, por inducción, queda frustrada. La sinrazón de mèden no se demuestra, porque es evidente, es un prejuicio aún más hondo que el del horror al vacío y, por tanto, ni siquiera es objeto de reflexión: “nada” no es pensable porque es lo que permite ponerse a pensar, que es como Ortega y Gasset define una creencia. Al llegar ahí, el argumento toca fondo (el fondo de la evidencia colectiva, de la opinión común) y rebota: por analogía a la “sinrazón” de “nada” se concluye la sinrazón del vacío.

Es el prestigio de un razonamiento matemático (y no el razonamiento mismo) el que lleva a una conclusión referente al mundo físico. Aristóteles no “ha demostrado” la imposibilidad de la nada matemática (¿el cero?) a partir de la evidencia de la nada física (el vacío), sino al revés: la evidencia del sinsentido de un impensable número cero (¿cómo van a ser “cero cosas” un caso de “cierto número de cosas”?) funda la imposibilidad física del vacío.

Los conceptos matemáticos (o la declaración de su sinsentido, como en este caso) y los modos de demostración dependen de los pre-juicios y creencias del grupo, a la vez que contribuyen a reforzarlos. Sentado esto, ya podemos pararnos a pensar en los particulares pre-juicios, aunque nos limitaremos aquí a dejar esbozados sólo algunos. Por un lado, un rasgo cultural específico: el sustancialismo o cosismo griego, el predominio del sentido de la vista que se forma “ideas” (abstractos) de las cosas. El número griego es así también algo lleno, pleno, visible: tanto en su versión pitagórica (números figurados), como en la platónica (“multitud de unidades”), como en la euclídeo-aristotélica (segmentos). Por otro lado, un rasgo socio-religioso específico de aquel mundo griego: la desazón producida por la pérdida de la fe en los dioses mueve a la especulación griega a construir un cielo de conceptos, principios y axiomas indudables bajo el que protegerse, y protegerse, en particular, del miedo al devenir, de ese brotar las cosas de la nada y volver a la nada cuando se renuncia a recursos trascendentes: ¿Cómo instalar entonces la nada en el corazón mismo de ese cielo protector que son las ideas y, en particular, las ideas matemáticas? No, para el cero no hay lugar .a-topos, “sin lugar”, es el término empleado por los matemáticos de entonces para declarar una conclusión como algo “imposible”) en el nuevo culto a la razón que estaba entonces sustituyendo en Grecia a la religión de sus mayores.

Ante el problema del vacío, el argumento aristotélico pone en funcionamiento ejemplarmente aquel dispositivo simbólico que analizaba Sperber (1978). Existe un problema (el del vacío y los cuerpos) mal conceptualizado y fuente de todo tipo de paradojas (como las de Zenón de Elea): un problema ante el que fracasa el dispositivo conceptualizador. Se produce una focalización sobre la imagen “nada/número” por desplazamiento analógico (“de igual modo que”: hòsper, “similarmente”). En torno a ese foco hay una condensación de evocaciones: en no ser del no-ser (y toda la aparición de partículas gramaticales negativas o privativas); la relación entre el punto y la línea como análoga a la relación entre la (im-) posible “nada” y el número; el número (aritmós) asociado a los cuerpos; la asociación “razón = relación (sumativa) = existencia”; horror al vacío; aparición del concepto de exceso o diferencia (que implica la exigencia de una sustrato común que permita sustraer = aphaíresis), etc. Se vuelve, por último, al problema inicial proyectando sobre él toda la cascada de evocaciones condensada en torno al foco.

Si ahora nos trasladamos a la China de la época de los Primeros Han, lo primero que choca no es ya encontrarse con el cero en el texto clásico más antiguo de la matemática China, Los nueve capítulos del arte matemático, sino con una multitud de ceros: unos que reciben distintos nombres según el contexto matemático en que aparecen (resolución de ecuaciones, cálculo de raíces cuadradas) y otros que aparecen en contextos que ni siquiera son matemáticos (técnicas adivinatorias, esquemas cosmogónicos). El cero está tan extendido en China como lo está en Grecia la aversión por él. Pero vayamos de nuevo a los textos mismos. En el capítulo 8 de Los nueve capítulos, el problema 8 dice:

Al vender 2 vacas y 5 cabras para comprar 13 cerdos, hay un superávit de 1000 monedas. El dinero obtenido de vender 3 vacas y 3 cerdos da justo para comprar 9 cabras. Al vender 6 cabras y 8 cerdos para comprar 5 vacas, hay un déficit de 600 monedas. ¿Cuál es el precio de una vaca, de una cabra y de un cerdo?

Hasta aquí, no parece haber nada nuevo. Pero la primera sorpresa surge al ver representado el planteamiento del problema: no en un espacio extenso como el euclídeo sino en un espacio simbólico, como el que desarrollará el álgebra matricial europea del siglo XIX. Pues bien, serán precisamente las características de estos espacios de representación las que den una realidad u otra, o incluso den o nieguen realidad, a lo que en ellos se representa. Será la re-presentación la que construya la presencia real de ciertos objetos, y no -como suele considerarse- a la inversa.

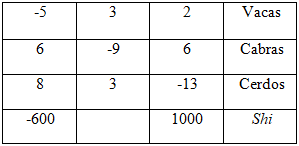
En la figura podemos observar una serie de características no matemáticas que, sin embargo, condicionan radicalmente cualquier intento de hacer matemática. Estas características atañen a las propiedades de cada lengua particular, a cierto modo de concebir el espacio de representación, y a la materia con la que se fabrican los números para colocarlos en el espacio de representación.

La disposición de la matriz reproduce la de la lengua china escrita: en columnas de arriba a abajo y de izquierda a derecha. Igual que la expresión de una ecuación en Occidente reproduce la estructura de las lenguas indoeuropeas (la segunda línea: 3x + 3z = 9y se corresponde con Sujeto-Verbo-Predicado: “3 vacas y 3 cerdos dan justo para 9 cabras”). Pero esta aparente trivialidad condiciona el que ciertas cosas puedan decirse y otras no, esto es, que ciertas cosas puedan existir entre los hablantes de una lengua y no existan para los de otra.

En la matriz, cada número (colección de palillos rojos o negros) significa en función del lugar que ocupa en el conjunto. No otra cosa ocurre con los ideogramas chinos, que son invariantes que adquieren un significado u otro según la posición que ocupan en la frase. Sólo teniendo a la vista el esquema global (como en una partitura musical) se entiende cada frase o cada palabra.

El “cero” de la segunda columna es, en el original, un hueco: en ese lugar no hay palillos (números). En nuestras lenguas, el hueco en la escritura es insignificante: se limita a separar dos significados, dos palabras (como hace también el hueco-silencio entre dos palabras habladas). Pero ese hueco en la escritura china es un hueco que significa: y significa lo que significa por ocupar precisamente ese lugar y no otro. (Por cierto, el que sea el lugar el que signifique y, por lo tanto, no haya la menor necesidad de atribuir un nombre especial –”cero”- al lugar vacío, ha llevado en ocasiones al flagrante etnocentrismo de decir que la China antigua desconocía el cero).

Si intentamos escribir esa columna en nuestra álgebra simbólica actual, resultaría: 3x - 9y + 3z = 0. Pero no encontramos expresiones así hasta nuestro s. XVII. Ni para los griegos, ni para el álgebra alejandrina, ni para la potente matemática árabe, ni para el álgebra renacentista, tiene el menor sentido que “algo” (el lado derecho de la ecuación) sea igual a “nada” (el lado izquierdo), es un absurdo que “nada” pueda predicarse de “algo”.

Junto a las características lingüísticas y a las del espacio de representación, el tercer elemento que permite al imaginario chino pensar el “cero” es el singular tipo de materialidad en que se expresa su sistema de numeración. El hecho de que los números no sean trazos-segmentos (como los de la geometría griega) ni piedras-cálculos (como los de la aritmética griega), sino que se constituyan al ubicar palillos en el tablero de cálculo, permite que, al operar, los palillos vayan cambiando de un lugar a otro, y que -en determinados momentos- determinados lugares queden vacíos de forma “natural”.

Pero si estos tres elementos (lenguaje, espacio simbólico de representación y palillos numerales) posibilitan el que pueda emerger algo como el cero, no determinan necesariamente esa emergencia. Son sólo un camino para que la nada pueda decirse, un camino que en el álgebra geométrica griega ya estaba bloqueado precisamente por las características específicas de esos tres elementos: un lenguaje lineal donde las palabras se remiten a conceptos externos (significados) en lugar de significar por sí mismas y por su situación en el contexto, un espacio extenso y homogéneo de representación y numerales alfabéticos que corresponden a medidas de segmentos o a cantidad de piedras o cuentas.

¿De dónde sacan entonces los matemáticos chinos la inspiración y el material con los que construir esos procedimientos y esos objetos que son imposibles para otros matemáticos, como los griegos o los renacentistas o incluso los de la Ilustración europea, tan sabios al menos como ellos? Ese manantial no es otro que la sociedad china de la época, con su peculiar estructuración social y conformación mítico-simbólica.

Una buena pista para adentrarnos en ese universo imaginario de la China anterior a los Han nos la suministran los propios palillos numerales. Los mismos palillos que se usan en álgebra son también los empleados en multitud de otras actividades, incluso populares: para leer el futuro, para reflexionar sobre la propia historia y la historia del pueblo chino mediante las técnicas del I Ching, para realizar cálculos comerciales, para jugar (con reglas no menos intrincadas que las del álgebra) y hasta para comer. En esos palillos está, precipitado, materializado, buena parte del imaginario social y de la memoria colectiva del pueblo chino. Por medio de los palillos la actividad matemática se funde, y se confunde, con otras mil actividades cotidianas.

Pues bien, en su uso algebraico, esos palillos son de dos colores (negro y rojo) o de dos formas (sección cuadrada o triangular), que se corresponden con lo que nosotros llamaríamos números negativos y positivos, respectivamente. Números que, como el cero, tampoco tienen el menor sentido ni para el álgebra geométrica griega ni para la potente álgebra simbólica árabe. No tiene el menor sentido afirmar, como hace algún ilustre historiador de la matemática como Boyer que “la idea de los números negativos no parece haber ocasionado muchas dificultades a los chinos, puesto que estaban acostumbrados a calcular utilizando dos grupos de palillos” (1986, p. 264). No tiene el menor sentido, pues una de dos: o la “idea de números negativos” es distinta de los grupos de palillos y los pre-existe en algún olimpo matemático, o ambas cosas - idea y palillos - son la misma cosa (lo que parece más acorde con el modo de pensar chino, para el que las ideas son directamente lingüísticas). En cualquiera de ambos casos el problema queda intacto: ¿por qué los chinos, y sólo los chinos, operan con palillos de dos colores, que nosotros podemos hoy identificar con nuestra idea de números positivos y negativos?

La respuesta la obtenemos observando atentamente cómo trabajan estos palillos en el álgebra fang cheng para la resolución de sistemas de n ecuaciones con m incógnitas (un método que no se conocerá en Europa hasta el s. XIX bajo el nombre de método de Gauss). El objetivo del método es ir emparejando (dui ze) y equilibrando (qi tong) entre sí palillos negros y rojos, de modo que se vayan destruyendo mutuamente (xiang xiao), hasta conseguir que determinados lugares queden vacíos, que en ellos los palillos desaparezcan (jin) (lo que en matemática moderna se llamaría diagonalizar la matriz). Literalmente, se trata de un sofisticado método para producir nada, para obtener el vacío, un método que pondría los pelos de punta a los griegos.

Si ahora enfrentamos esto con la batería de argumentos con que Aristóteles, y toda la tradición occidental (matemática, estética, física, teológica), intenta expulsar al vacío del ámbito de lo pensable y de lo existente, acaso tenga sentido pararse a pensar en que estamos no sólo ante dos matemáticas inconmensurables, sino ante dos modos de pensar que no admiten común medida (y soy consciente del rechazo general que producen tesis como éstas, un rechazo que también sería interesante analizar en el marco de una antropología simbólica de los mitos modernos de Occidente).

Pero lo realmente interesante (aunque ahora no podamos detenernos en ello) es observar la perfecta homología que entrelaza a la terna matemática zheng/fu/wu (palillos-rojos/palillos-negros/hueco-en-el-tablero) con la terna simbólica yang/yin/tao. Una terna en torno a la que se anuda todo el complejo de significaciones imaginarias chinas y que alimenta tanto el vocabulario como los modelos teóricos de los saberes chinos: filosofía, física y química, geografía, astronomía, etc. Una terna que Granet (1968) ha estudiado magistralmente en su doble dimensión de dar forma a - y también expresar - las distintas dimensiones y dinamismos de la vida social en China: fiestas populares, disposición de las habitaciones de la casa, formas de gobierno de las comunidades locales, etc. El tao, como el hueco en el tablero de cálculo, se nombra siempre negativamente (bien mediante imágenes contradictorias, bien diciendo lo que no es). El tao divide -a la vez que enlaza- a las oposiciones en que consiste toda realidad (y, en particular, la realidad del número). Es la bisagra que articula y permite el tránsito y la operación entre los opuestos, es el manantial del que emergen las alternancias y las oposiciones y el lugar sin marca en el que se remansan. Un estudio filológico detallado de esta homología confirma rotundamente el singular arraigo de la matemática china - y también de su lógica - en las mismas formas de memoria compartida que estructuran y dinamizan toda su vida social (por ejemplo, los significados de zheng y fu en el lenguaje ordinario, o el carácter no-marcado de lo negativo respecto de lo positivo).

Todo este complejo es el que resulta focalizado cuando el algebrista chino se enfrenta con lo que nosotros hoy llamaríamos el “cero”. Ahora bien, aunque puede decirse que, en cierto sentido, tanto Aristóteles como Liu Hui afrontan el mismo problema (el de encontrar un equivalente numérico de un vacío físico, sea éste un no-ser o un hueco en el tablero), no es menos cierto que tanto el propósito como el magma imaginario de cada uno es muy distinto. En cuanto al propósito, el griego trata de mostrar que tal vacío es imposible y, para ello, parte de la evidencia de que su equivalente matemático no tiene ningún sentido. Para el chino, por el contrario, lo evidente es el hueco vacío que él observa en el tablero de cálculo, pero como ese hueco pertenece a un tablero de cálculo, debe tener necesariamente un sentido en el cálculo: debe ser también un número como todos los demás que están en el tablero. El quid de la situación está, por tanto, en lo que a cada uno se le presenta como evidente, lo que cada uno da por des-contado y le permite –o le impide- ponerse a contar. Eso que se da por des-contado afecta a los dos dominios que aquí están en juego: lo que se cuenta, es decir, los números (dominio aritmético) y lo que se cuenta, es decir, las narraciones (dominio lingüístico). Por eso el primero no puede decir nada sobre lo que nada es (el “cero”/vacío), mientras que el segundo ve el hueco como un número con la misma plasticidad con que tantas narraciones taoístas que él ha oído hablan de la potencia del vacío y de su papel como gozne o quicio que articula los opuestos.

Esas evidencias (lo que se da por des-contado), pre-su-puestos (lo que se pone previamente debajo) o pre-juicios (lo que es previo a la emisión de cualquier juicio) son las que se han movilizado ante el problema inicial y han resultado evocadas al focalizar este sobre la imagen que lo simboliza. Ya vimos cómo se concretaba en Aristóteles ese proceso de simbolización. En el caso de Liu Hui pueden observarse los mismos pasos, pero ahora modelados por el imaginario de su cultura:

• se parte de un problema semejante: cómo conceptualizar y manipular el vacío,

• se focaliza también sobre un posible correlato matemático de ese vacío: el que nosotros podríamos llamar “cero”,

• se condensa una cascada de evocaciones sobre este foco,

• se desplazan de nuevo al problema inicial estas evocaciones, lo que permite dar al problema cierta forma y cierta posibilidad de manejo.

La diferencia radical entre uno y otro matemático se da en el paso (c) de este proceso simbolizador, pues las evocaciones que el imaginario de Liu Hui le trae a la mente hablan de: la asociación del vacío o el no-ser (wu) con el tao (al que los clásicos siempre se refieren mediante partículas gramaticales negativas) y del tao con el poder-ser; la capacidad de significación del lugar (aunque ese lugar esté vacío); la disposición matricial de los números análoga a la disposición de las frases en la escritura china; la atracción –y no horror- hacia un vacío que incluso se intenta provocar.

Reflexiones finales

Para desentramar ciertos nudos del imaginario el recurso al análisis de las metáforas presentes en los textos matemáticos se revela en su capacidad heurística. El análisis a partir de las metáforas viene a coincidir con el que hasta aquí hemos desarrollado utilizando el dispositivo de simbolización que plantea Sperber. Los movimientos de focalización, condensación y regreso al problema inicial son otros tantos movimientos metafóricos, donde los significados –y los valores, emociones y asociaciones a ellos vinculados- circulan de un ámbito a otro, que es la característica específica de los significados metafóricos.

Baste dejar aquí otro apunte de cómo la potencia de la metáfora extractiva en nuestro imaginario condiciona nuestro razonamiento matemático. Cuando la teoría de conjuntos parecía poder venir a sacar a las matemáticas de la fragmentación a que la habían abocado tantas especialidades desconectadas entre sí, la aparición de las famosas paradojas amenazó con arruinar ese precioso edificio formal unificador (Kline, 1985). Una de estas paradojas es la que resulta de observar que si del conjunto de los números naturales N extraemos el conjunto de los números pares P, el conjunto resultante es estrictamente menor, pues ese resto está formado por el conjunto de todos los números impares I. Pero, por otro lado, si en vez de apelar a ese modelo extractivo, apelamos al modelo de emparejamiento propio de un imaginario como el chino, nos encontramos con que puede establecerse una correspondencia biunívoca entre N y P, por lo que ambos conjuntos tendrían el mismo número de elementos. Así, según enfoquemos el problema desde el marco impuesto por una u otra metáfora, obtenemos conclusiones incompatibles. D. Bloor (1988) ofrece un bello análisis de cómo se evitó el desastre recurriendo a un expediente tan poco formal como es la negociación de una nueva definición de conjunto que integrara ambos marcos y disolviera la paradoja.

El análisis metafórico de los conceptos y problemas matemáticos nos ofrece así una doble vía para insertarlos en el lenguaje y en el mundo cultural del estudiante. Por un lado, permite a éste abordar las matemáticas en un contexto del que él forma parte, evitando la sensación de extrañeza que tan a menudo le paraliza. Por otro, puede percibir que las matemáticas no sólo forman parte de mundos más amplios, sino que son un instrumento privilegiado para comprender mejor esos otros mundos, como hemos podido hacer aquí con los mundos griegos y chino, a los que espero que estas líneas hayan ayudado a conocer un poco mejor.

Referencias bibliográficas

Bloor, D. (1998). Conocimiento e imaginario social. Barcelona: Gedisa.

Boyer, C. B. (1986). Historia de la matemática. Madrid: Alianza.

Granet, M. (1968). La pensée chinoise. Paris: Albin Michel.

Kline, M. (1985). Matemáticas. La pérdida de la certidumbre. Madrid: Siglo XXI.

Lizcano, E. (1993). Imaginario colectivo y creación matemática. La construcción social del número, el espacio y lo imposible en China y en Grecia. Barcelona: Gedisa.

Lizcano, E. (1999). La metáfora como analizador social. Empiria, 2, 29-60.

Lizcano, E. (2006). Metáforas que nos piensan. Sobre ciencia, democracia y otras poderosas ficciones. Madrid: Traficantes de Sueños.

Lizcano, E. (2009a). La economía como ideología. Un análisis socio-metafórico de los discursos sobre “la crisis”. Revista de Ciencias Sociales, 1(16), 85-102.

Lizcano, E. (2009b). Hablar por metáfora. La mentira verdadera (o la verdad mentirosa) de los imaginarios sociales”, Sociedad, 28, 167-190.

Ortega y Gasset, J. (1979). La idea de principio en Leibniz y la evolución de la teoría deducativa. Madrid: Alianza Editorial.

Sperber, D. (1978). El simbolismo en general. Barcelona: Anthropos.

Szabó, A. (1964a). The Transformation of Mathematics into Deductive Science and the Beginnings of its Foundation on Definitions and Axioms. Part. 1. Scripta Mathematica, 27(1), 27-49.

Szabó, A. (1964b) The Transformation of Mathematics into Deductive Science and the Beginnings of its Foundation on Definitions and Axioms. Part. 2. Scripta Mathematica, 27(2) 27, 3-139.

Notas

Obra bajo Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional